An informal history of the Prime Gap List

Origins and development of the computational search for first known occurrence prime gaps

May 6, 2021 • Graham Higgins • ~ 23 min to read • post

Introduction and background

The history of the prime gap list of today begins back in the last year of of the 20th Century when Dr. Thomas R. Nicely created a web site to curate some papers on first occurrence prime gaps that he submitted to the AMS (American Mathematical Society) and to make available an openly-accessible “electronic” version of the list of first known occurrence prime gaps.

Tom Nicely began publishing lists of record prime gap data on his web site in May 1999 and maintained the lists until his death in a car accident on 11th. September 2019. Prior to his retirement, Dr. Nicely was professor of mathematics at the University of Lynchburg. The Internet Archive’s “Wayback Machine” has captured the Univerity‘s Remembering Dr. Thomas Nicely page.

The first paper is by Thomas R. Nicely and Bertil Nyman, “First occurrence of a prime gap of 1000 or greater”, submitted 26 May 1999 to Math. Comp. Nicely’s calculations were performed during the period October, 1997, through February, 1999; Nyman’s between August, 1998, and May, 1999. The second paper is by Thomas R. Nicely, “New maximal prime gaps and first occurrences”, Math. Comp. 68:227 (July, 1999), 1311-1315. MR 99i:11004. Calculations performed during the period August, 1995, through October, 1997.

Description of the prime gap list

The following rubric, taken from archive.org’s first capture and headlined “Last updated 3 September 2000” describes and qualifies the content of the list.

The following table is believed to exhibit all first occurrence prime gaps conclusively established as of the date shown above.
Gaps indicated in parentheses are first known occurrences likely to be, but not yet definitively established as first occurrences.
Gaps indicated in square brackets are first known occurrences which are not believed to be first occurrences.
Maximal gaps are marked with an asterisk (\*).
All prime gaps in $0 < x < 1.2161 × 1016$ have been scanned.
The smallest gap whose first occurrence remains uncertain is the gap of 968.
No gap exceeding 1132 has been established as a first occurrence.
Nyman’s count of primes below 1016 exceeded the accepted value of $pi(1016)$ by 809, a notable discrepancy. However, analysis indicates a probability of less than one in one million that this caused an error (specifically, an omission) in his compilation of prime gaps; this computation presumes a uniform distribution of false primes, and the probability of error is otherwise somewhat greater. Nicely has independently checked all gaps occurring between $7.2 × 1013$ and $2.75 × 1015$ .
The listed discoverers and dates reflect the most accurate values known for the actual date of discovery; if this is not known, the date of publication or the date of the preprint is shown; if this is not known, an estimate is given. Some or all of the gaps occurring below 105 were almost certainly known prior to the indicated discovery, and the correct attribution of some of the other gaps below 108 is in doubt.
The convention is followed here that the size $G$ of a gap is the difference of its two bounding primes; consequently a gap $G$ contains $(G - 1)$ consecutive composite integers (some authorities take $(G - 1)$ itself as the size of the gap).
Note that the term *first occurrence prime gap* (of measure $G$ ) refers to that interval $p <= x <= p+G$ for which (1) $p$ and $p+G$ are primes, (2) $p+t$ is composite for each integer $t=1,...,G-1$ , and (3) no smaller positive prime $p$ possesses these properties. The entity might be more accurately described as the earliest or smallest occurrence of the gap $G$ , but the terminology first occurrence prime gap is well established in the literature.
Notification of any errors or omissions will be appreciated.

Rationale for a list of first occurrence prime gaps

Nicely and Nyman’s work was conducted in the context of general interest by number theorists in attempting to formalise the distribution of prime numbers. As Dr. Nicely observes: “The study of the distribution of the prime numbers among the positive integers occupies a central place in number theory.”

The number of primes up to $x$ , denoted by $π(x)$ , is roughly $x/log(x)$ for large values of $x$ ; this is the celebrated Prime Number Theorem. Therefore, if we randomly choose an integer near $x$ , then it has about a 1 in $log(x)$ chance of being prime.

In other words, as we look at primes around size $x$ , the average gap between consecutive primes is about $log(x)$ . As $x$ increases, the primes get sparser and the gap between consecutive primes tends to increase.

Here are some natural questions about these gaps between prime numbers.

Do the gaps always remain roughly about size $log(x)$ or do we sometimes get unexpectedly large gaps and sometimes surprisingly small gaps?

Can we say something about the statistical distribution of these gaps? That is, can we quantify how often the gap is between, say, $α log(x)$ and $β log(x)$ , given $0 ≤ α < β$ ?

Except for the primes 2 and 3, clearly the gap between consecutive primes must be even. Does every even number occur infinitely often as a gap between consecutive primes? For example, the twin prime conjecture says that the gap 2 occurs infinitely. How frequently should we expect the occurrence of twin primes?

From the introduction of Kannan Soundararajan’s “Small gaps between prime numbers: the work of Goldston-Pintz-Yıldırım” Bull. Am. Math. Soc. New Series. 44 (1): 1–18

Context for construction of a list of first occurrence prime gaps

Dr. Nicely’s list of references provides some more details about the context - “No general method more sophisticated than an exhaustive search is known for the determination of first occurrences and maximal prime gaps. As in the present study, this is most efficiently done by sieving successive blocks of positive integers for primes, recording the successive differences, and thus determining directly the first occurrences and maximal gaps.”

Dr Tom Nicely’s table of first occurrence prime gaps

The first couple of dozen entries, as published in August 2000:

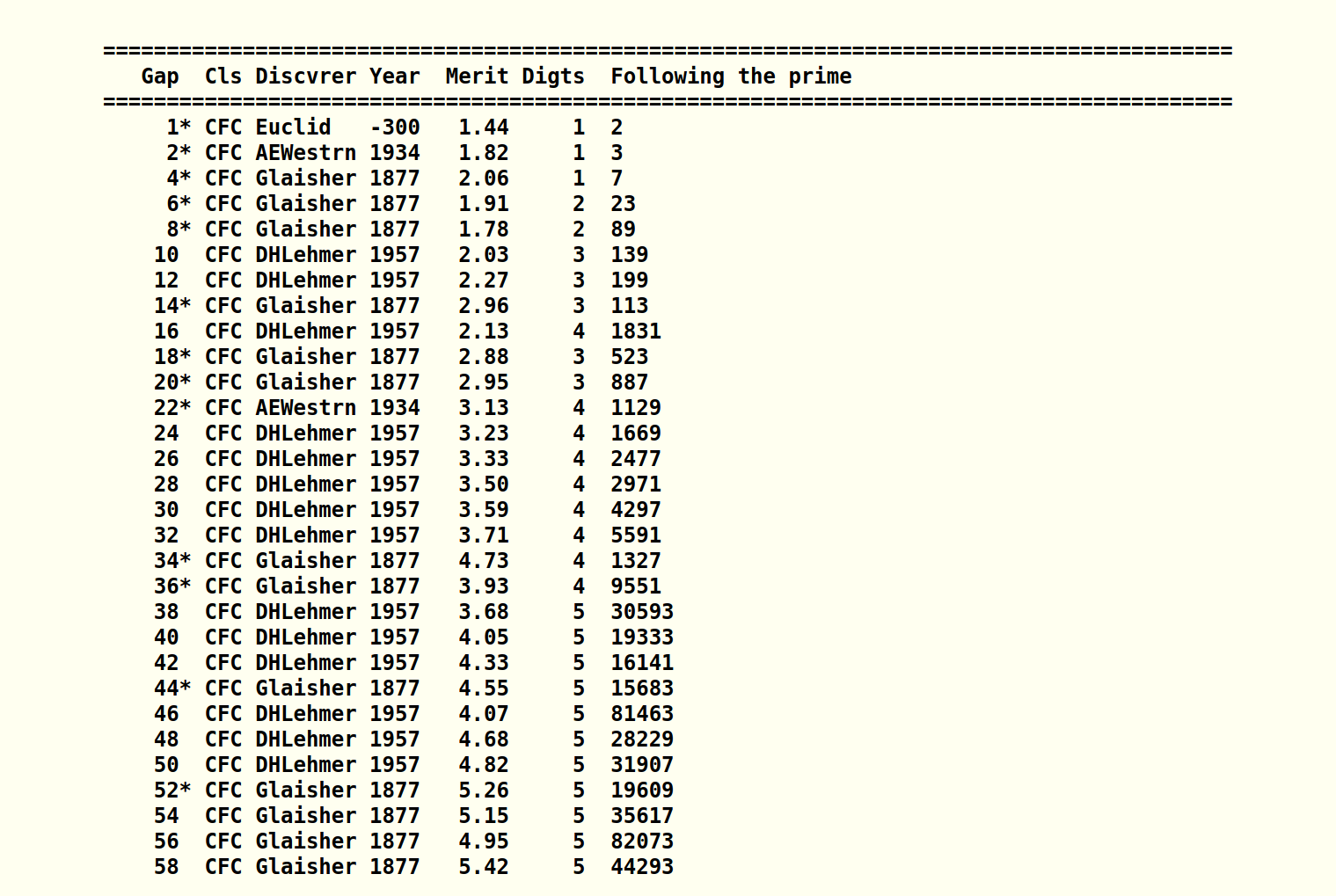
Nicely’s prime gap list

And some comments and observations on the above content …

Hand-generated tables

And while both Nyman’s and Nicely’s calculations were performed on Pentium series machines, there’s a long history, dating back at least as far as Glaisher’s dedicated efforts by hand, reported in 1877:

J. W. L. Glaisher, "On long successions of composite numbers" Messenger of Mathematics 7 (1877), 102-106, 171-176

And in 1934 A. E. Western provided a hand-calculated table of gaps between successive primes in A. E. Western, “Note on the magnitude of the difference between successive primes”, London Math. Soc, v.9, 1934, p.276-278 (unfortunately, Western’s data is inaccessible behind a John Wiley & Sons, Inc paywall).

The early digital computing era

Dr. Nicely notes that the technique of exhaustive search “has been used by Shanks, Lander and Parkin, Brent, and Young and Potler.”

Both Glaisher’s and Western’s hand-produced tables were referenced by Shanks but by 1964, the long hours of searching through primes had been devolved to the digital computer and Dr Nicely’s references echo the developments in processing over the decades:

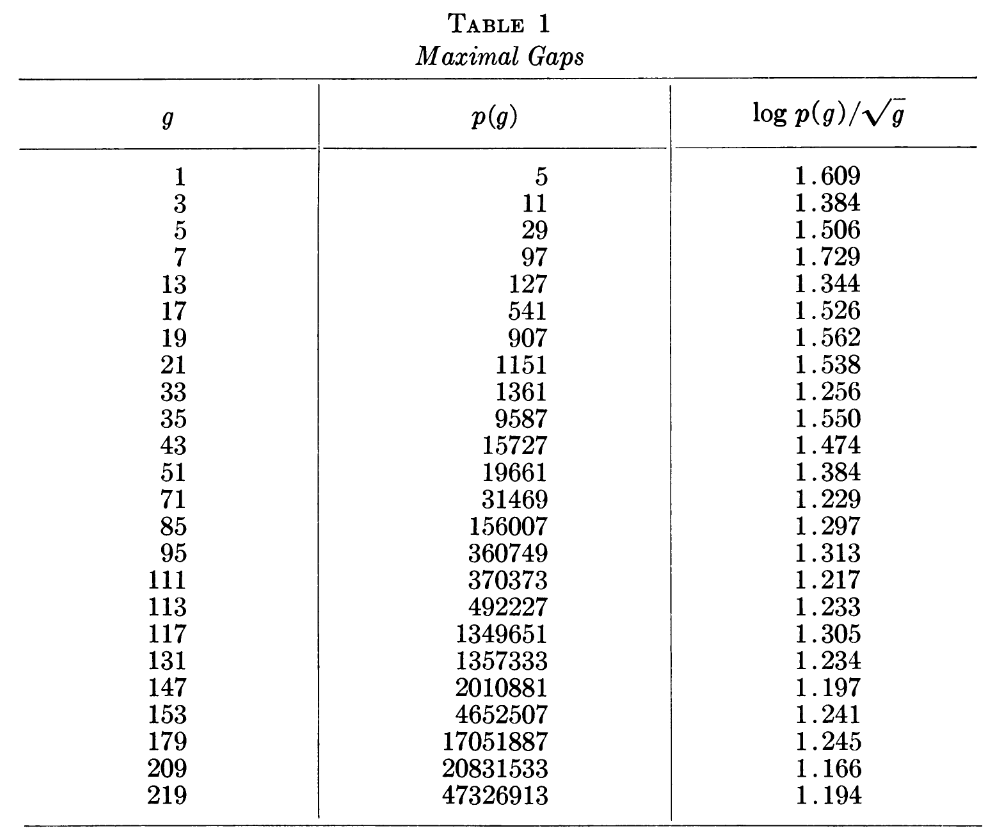
Daniel Shanks, "On maximal gaps between successive primes" Math. Comp. 18 (1964) 646-651. MR 29:4745.

In 1964, Daniel Shanks was working at the US Navy’s David Taylor Model Basin (test facilities for ship design) where they had one of two UNIVAC LARCs produced. Shanks summarised the available results: “Empirically, the exact facts are known out to $g = 209$ thanks to an often-quoted but still not published study of D. H. Lehmer concerning the distribution of primes out to $37•10$ ⁶. Previously, less complete tables were given by Western and by Glaisher.”

D. H. Lehmer, "Tables concerning the distribution of primes up to 37 millions" 1957, mimeographed copy deposited in the UMT File and reviewed (by J. L. Selfridge of IBM Research, Yorktown Heights NY) in MTAC, v.13, 1959, p.56-57

The tables may well have have been produced in association with a study of the primality of Mersenne numbers performed on SWAC, a parallel computer using a Williams tube memory and the fastest computer in existence at the time.

Several references to foundational work are unavailable for casual inspection, such as D. H. Lehmer’s list, Kenneth I. Appel and J. Barkley Rosser’s “Table for Estimating Functions of Primes” and F. J. Gruenberger and G. Armerding’s, “Statistics on the first six million prime numbers”.

Fortunately, in his paper, Shanks provides the first accessible version of the prime gap list - “From these results (slightly reinterpreted) we have given in Table 1 a list of maximal gaps up to $g=219$ .”

Shanks’ prime gap list

The supercomputer era

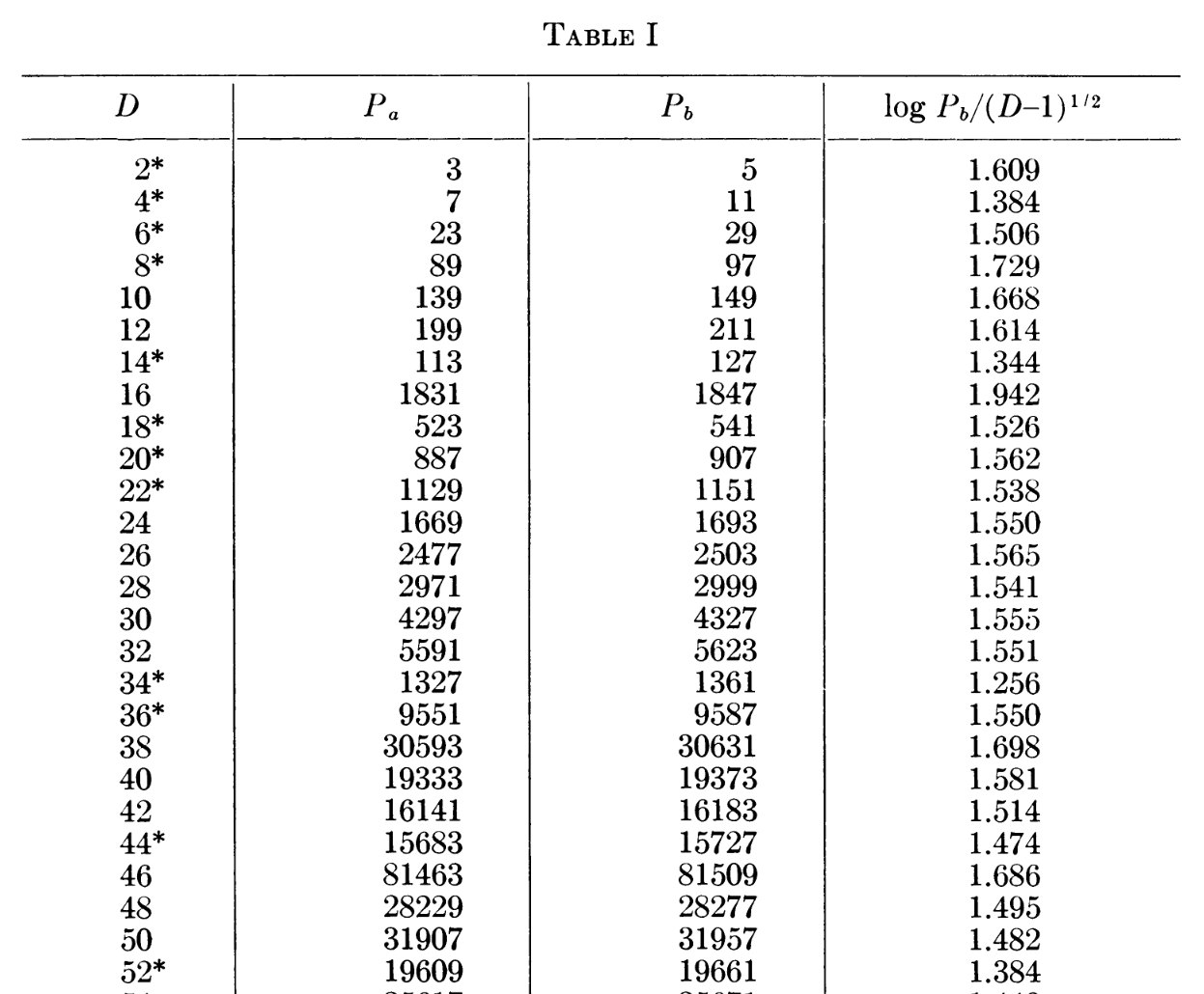
L. J. Lander and T. R. Parkin, "On First Appearance of Prime Differences", Math. Comp. 21 (1967) 483-488. MR 37:6237.

“A program for the CDC 6600 was written to implement a sieve technique for generating and examining gaps in primes. ... Table I for $1.46 x 10$ ⁹ < P < 1.096 x 10¹⁰ presents the results obtained from this program.”

Generally considered to be the first successful supercomputer, the CDC 6600 was the world's fastest computer from 1964 to 1969.

Lander and Parkin‘s table of gaps in primes is clearly closer in format to Nicely’s table:

L. J. Lander and T. R. Parkin report: “In private correspondence Daniel Shanks suggested the possibility of extending Table I in [2] over the new differences found. Accordingly, Table I shows $log P$ _b/(D — l)^1/2, with each maximal gap $D$ marked with an asterisk. Maximal gaps, according to Shanks, are those larger than any preceding gap in the sequence of primes.”

Lander and Parkin’s prime gap list

Richard P. Brent, "The first occurrence of large gaps between successive primes" Math. Comp. 27:124 (1973) 959-963, MR 48#8360.

“The computations were performed on an IBM 360/91 computer at the IBM T. J. Watson Research Center. ... efficiently scanned for large gaps by an algorithm”

The IBM System 360 Model 91 was the world's biggest, fastest, and most powerful computer in the mid-to-late 1960s, designed to handle high-speed data processing for scientific applications.

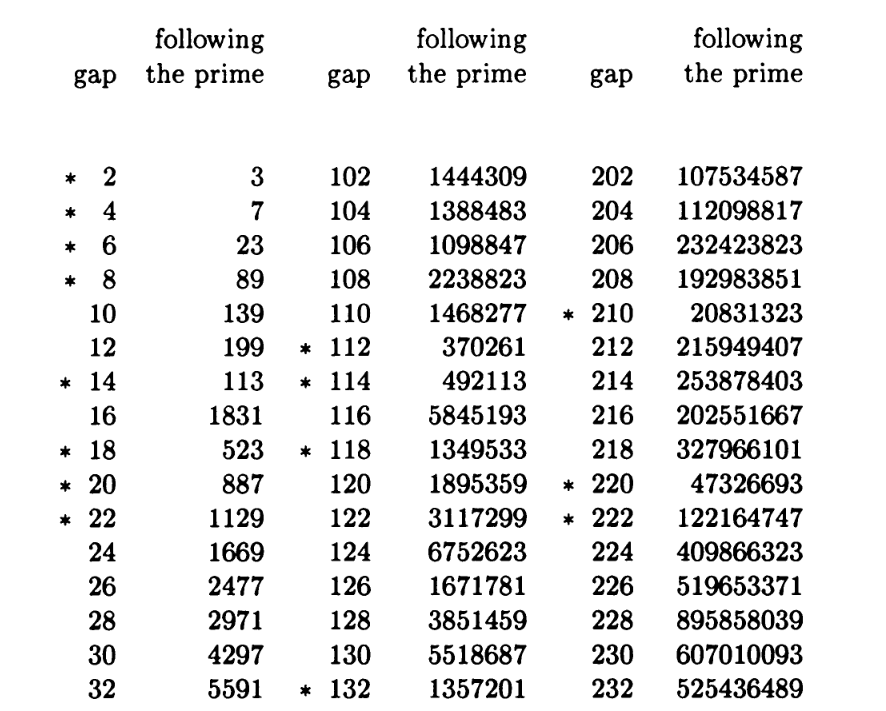
Jeff Young and Aaron Potler “First occurrence prime gaps” Math. Comp. 52:185 (1989) 221-224. MR 89f:11019.

“An ongoing search for first occurrence prime gaps is being carried out which extends all previous work done on this subject. To date this search has found all such gaps for primes up to $7.263 x 10$ ¹³. First occurrence prime gaps had previously been known for primes less than 4.444 x 10¹². Computer programs were written ... on a CRAY-2 supercomputer.”

The Cray-2 supercomputer was the fastest machine in the world when it was released.

Young and Potler‘s table of gaps in primes is even closer in format to Nicely’s table:

“The following table lists all the first occurrence prime gaps found. This table agrees with all previously published results (Brent and Lander & Parkin). The maximal first occurrence prime gaps are marked with an asterisk (*).”

Young and Potler‘s table of gaps in primes

The microcomputer era

1999

Young and Potler’s 1989 work was the last extension to the list of prime gaps for a decade.

Thomas R. Nicely and Bertil Lyman continued the work in the mid-1990s, distributing the search across a number of Pentium II PCs and on 26 May 1999 they submitted a(n unaccepted) report on progress to Math. Comp. — Thomas R. Nicely and Bertil Nyman, “First occurrence of a prime gap of 1000 or greater”.

Nicely successfully submitted a second paper in July of the same year, observing: “Calculations performed during the period August, 1995, through October, 1997”.

Thomas R. Nicely “New maximal prime gaps and first occurrences” Math. Comp. 68:227 (July, 1999), 1311-1315. MR 99i:11004.

“The search for prime gaps is being carried out as part of a larger program ... All computations are being executed during slack hours on personal computers belonging to the author or assigned to the Department of Mathematics at Lynchburg College. The number of systems (most of them Pentiums) in use has averaged about fifteen since the present program began in 1993. ... Typical throughput is about 10¹¹ integers per day on a 60 MHz Pentium.”

Gateway 2000 Pentium II

“The search for first occurrences of prime gaps, and maximal prime gaps, is extended to 10¹⁵. New maximal prime gaps of 806 and 906 are found, and sixty-two new first occurrences are found for gaps varying in size from 676 to 906.”

“Thus all first occurrences of gaps through 674, as well as scattered first occurrences for gaps through 778, were tabulated, and all maximal prime gaps through 778 were located. In addition, Young and Potler continued their calculations to an unpublished higher level; Ribenboim [13, p. 142] credits them with the discovery of an additional maximal prime gap of 804 following the prime 90874329411493, and this was privately confirmed by Young.”

First online publication of a comprehensive table of first known occurrence prime gaps

In May 1999, Nicely published the complete list of first known occurrence prime gaps along with the discoverer, the year of discovery, the merit of the gap, the number of digits in the starting prime and the starting prime itself as a plaintext list in HTML. Maximal gaps were denoted with an asterisk and the status of the bounding primes (confirmed or probable).

The prime gap list as published by Nicely in May 1999 runs to just over 500 entries. Dr. Nicely collated all of the previously-published prime gap lists (including Glaisher’s list from 1887, Western’s list from 1934, Lehmer from 1957, Appel and Rosser from 1961, Lander and Parkin from 1967, Brent from 1973 and Young and Potler from 1989) as well as the additional discoveries made by Nicely and Lyman.

1999-2019 the era of collaboration

For the first couple of years after the initial publication of the electronic version of the first known prime gap list, there were only few changes to Bertil Nyman’s entries and one submission in mid-2001 from Gilles Blanchette in Montreal.

However, by February 2002, Dr Nicely had collated a large number of additions from different sources, a 1992 submission to the Letters of Journal of Recreational Mathematics by D. Baugh and F. O’Hara but mainly from a small handful of contributors: Harvey Dubner who had been in contact with Nicely since 1996, Kenneth Conrow of Kansas State University and a number of others working privately - Jim Fougeron, Kjell-Olav Grøndalen, Nuutti Kuosa and Luis Rodriguez.

Dubner and Conrow (mainly Dubner) added over 2000 entries to the the list, rendering it unwieldy as a single publication and Nicely created a second list “First known occurrence prime gaps (exceeding 1132)”.

By early 2003, the list of first known occurrence prime gaps had been split into five parts; the number of entries had grown to 5550 (with Dubner and Nicely contributing the majority, supported by contributions in the > 9999 range by R.Athale and J.L.G. Pardo) with the largest gap discovered 233822, following a prime of 5878 digits in length.

Additional work and contributions continued, by August of 2003 Jens Kruse Andersen has contributed over 1500 records of gaps > 11999 and the the number of separate sub-lists had grown to eight. Later that year, Hans Rosenthal joined Andersen in making significant contributions to the upper reaches and the number of sub-lists was extended to ten to cover gaps exceeding 19999.

By the middle of the following year, there were fifteen sub-lists, extending to “1000000 to 999999998” with a couple dozen contributors now emailing submissions to Nicely for inclusion in the list.

Eventually, the number of sub-lists grew to twenty-one and in early 2016 Dr. Nicely collated them all into a single file: “The complete, untruncated listing of all presently known first occurrence and first known occurrence prime gaps is available as allgaps.dat (9 MB), a Win/DOS text file describing one gap per line, in the standard format.”

At this stage, the table of first known prime occurrence prime gaps had 84,629 entries and the largest gap discovered was 4680156, following the prime number $230077#/2229464046810 - 3131794$ (99750 digits in length), discovered by Martin Raab in 2016.

Gapcoin contributions

The first contribution from the Gapcoin network (as recorded by archive.org) appears in the list of first known occurrence prime gaps 4000-5998 for April 2015 which include 519 entries credited to Gapcoin.

It’s doubtful that any of these entries filled any gaps in new first known occurrences and far more likely they were improvements in merit of existing first known occurrences, such as that for the gap 4622.

The merit of the 2015 Gapcoin discovery was 24.24 whereas the existing entry, discovered by Helmut Spielauer in 2014, was of merit 24.03:

+  4622  C?C Gapcoin  2014  24.24    83  64051350512724708215555131043627811252980984635815736414841611370833453628776789829
-  4622  C?C Spielaur 2012  24.03    84  334636025237567784523020021022819575015790229177281468713072013451084022710943448127

Spielaur’s 2014 entry is an improved merit over Torbjörn Alm‘s 2004 discovery

+  4622  C?C Spielaur 2012  24.03    84  334636025237567784523020021022819575015790229177281468713072013451084022710943448127
-  4622  C?C TorAlmJA 2004  20.69    98  10298668143351087376700838989365136734283548190197588211113508946614970440606700979807555048843691

And that itself is an improvement in merit over H. Dubner’s 2002 discovery:

+  4622  C?C TorAlmJA 2004  20.69    98  10298668143351087376700838989365136734283548190197588211113508946614970440606700979807555048843691
-  4622  C?C H.Dubner 2002  15.95   126  680941728113890909988182383034816373412341103196700637318249591357089162624656291902634885080827820797742072433863223714372631

2019 end of an era

On Wednesday, September 11, 2019, Dr. Thomas R. Nicely died as a result of injuries sustained in a car accident. In the last update of August 2019, Dr. Nicely offered the following summary of the list of known first occurrence prime gaps:

“All prime gaps in $0 < x < 2$ ⁶⁴ have now been analyzed, where 2⁶⁴ = 18446744073709551616, the smallest positive integer requiring more than 64 bits in its binary representation (i.e., not representable in C as a uint64_t).

The final push from 18446744000000000000 to $2$ ⁶⁴ was carried out by the combined efforts of PGS members Jerry LaGrou, Dana Jacobsen, Robert Smith, and Robert Gerbicz. No gap exceeding 898 was found in this interval.

Calculations beyond 2⁶⁴ will be hindered by the fact that their binary representations require more than 64 bits, exceeding the capacity of the hardware registers in most present-day numeric processor FPUs (supercomputers excepted) and forcing the computations into software. This can be expected to reduce speed and throughput by one or two orders of magnitude.

The upper bound of exhaustive analysis of gaps has been extended successively, as follows. For the most recent results, see the Prime Gap Searches project at the Mersenne Forum (see PGS in the Bibliography for a list of the participants). Most of the calculations beyond 16000e15 were carried out by Thomas Ritschel.”

The last prime gap list published by Nicely ran to 96,476 entries with the largest gap being 6582144 following the prime number $499973#/30030 - 4509212$ (216841 digits in length), this time discovered by Martin Raab in 2017.

2020 beginning of a new era of community curation

Since 2013, members of the Mersenne Forum’s Prime Gap Search Group (PGS) had been communicating and collaborating with Dr. Nicely in checking and validating submissions to the prime gap list, so it was natural that the PGS would concern itself with the preservation of Dr. Nicely’s work and its contribution to number theory.

“Robert G is right to say this needs to be automated. All that is needed is a simple upload mechanism and checking program with a web page showing the record gaps and a download facility for reports. All we need is a person to create the script.” Rob Smith, in a post to the Mersenne Forum Prime Gap Search Group.

Prime gap list Github repository

A Github repository curating the list of first known occurrence prime gaps

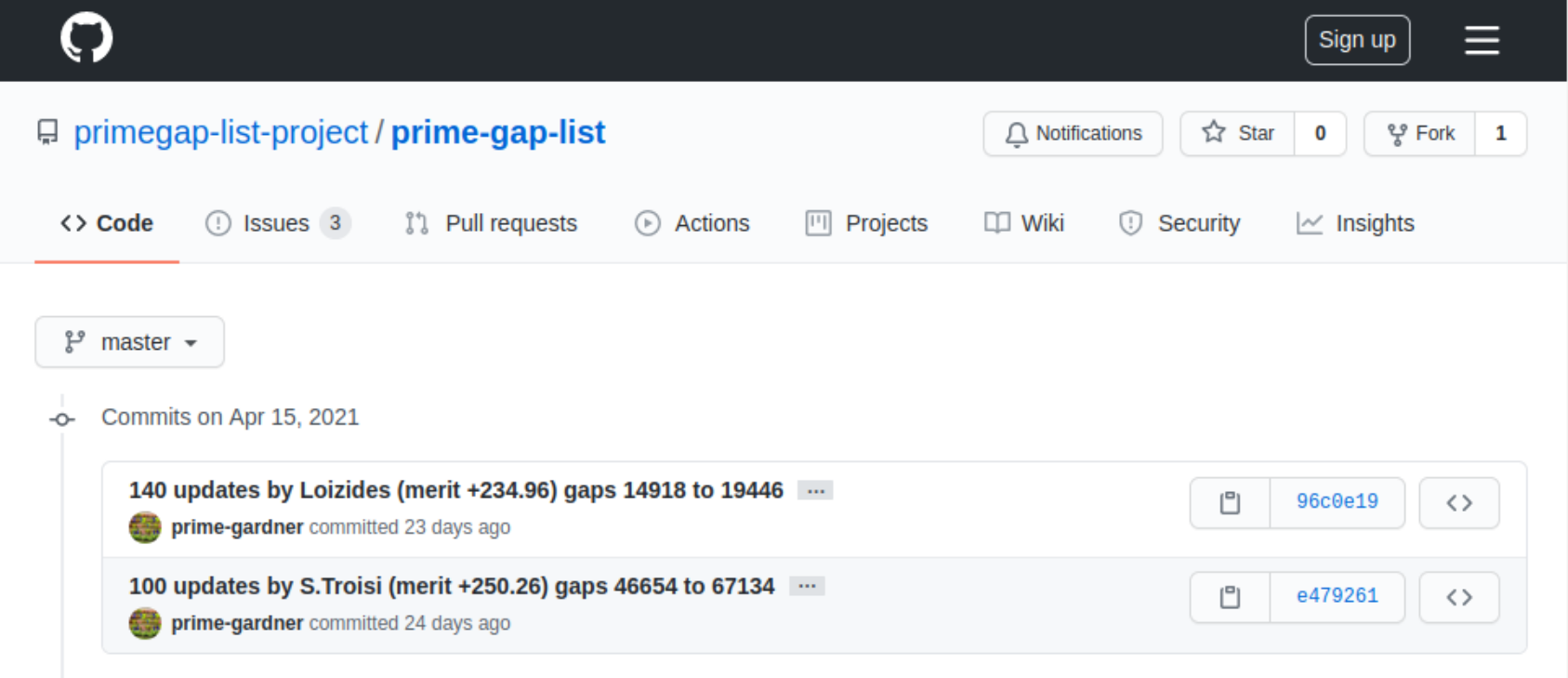
The result of the exercise was the creation of a Github repository which preserved the successive publications of Dr. Nicely’s allgaps.dat list as successive commits to the repository, transcribed as SQL insert statements, creating a downloadable SQLite3-compatible database for convenient analysis.

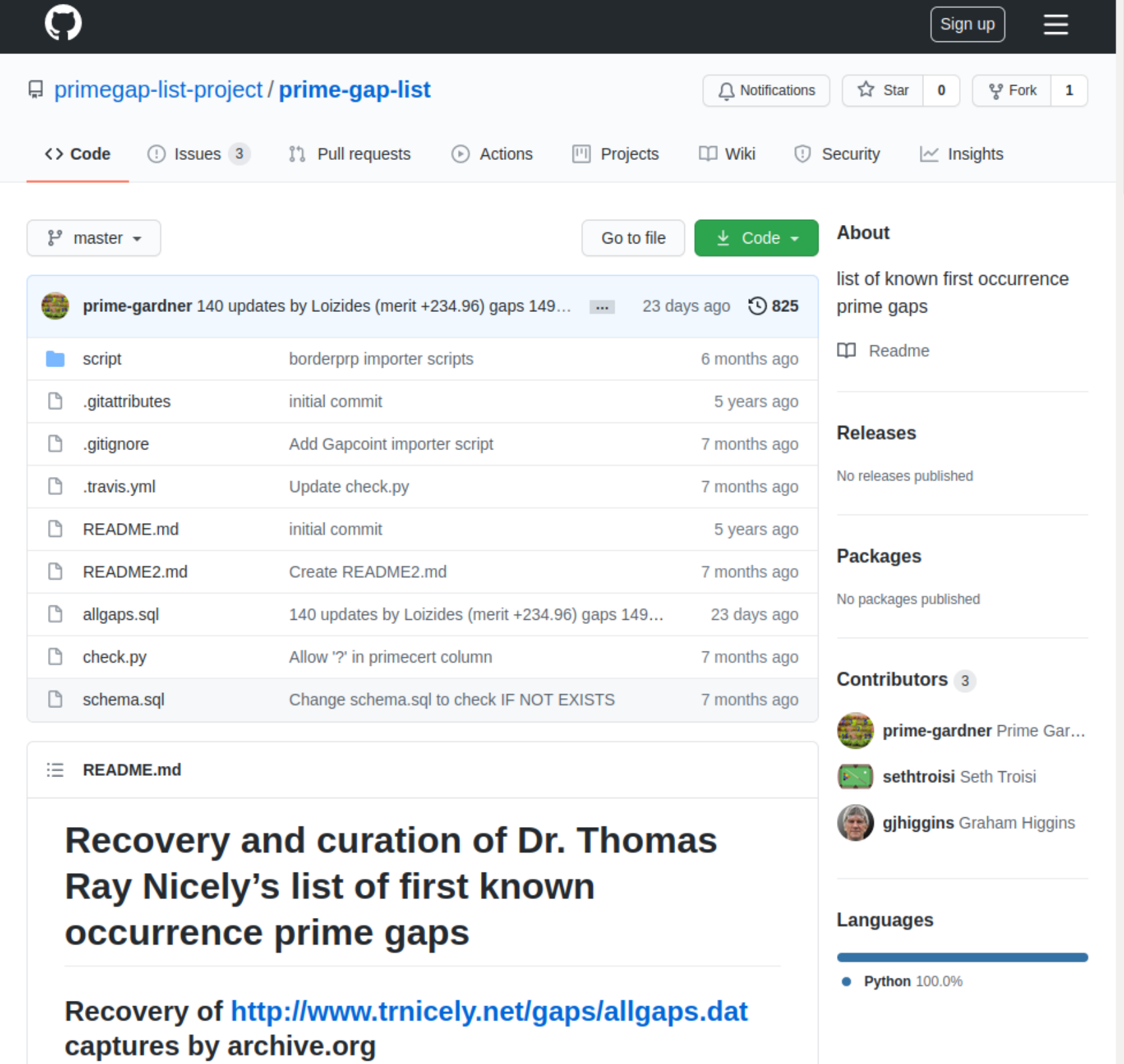
Screenshot of the prime gap list Github repository

One contextually-valuable aspect of open source repository technology is that successive changes to the content are made clearly visible, in this instance preserving the credit for previous contributions which would otherwise be lost with a continually-updated list:

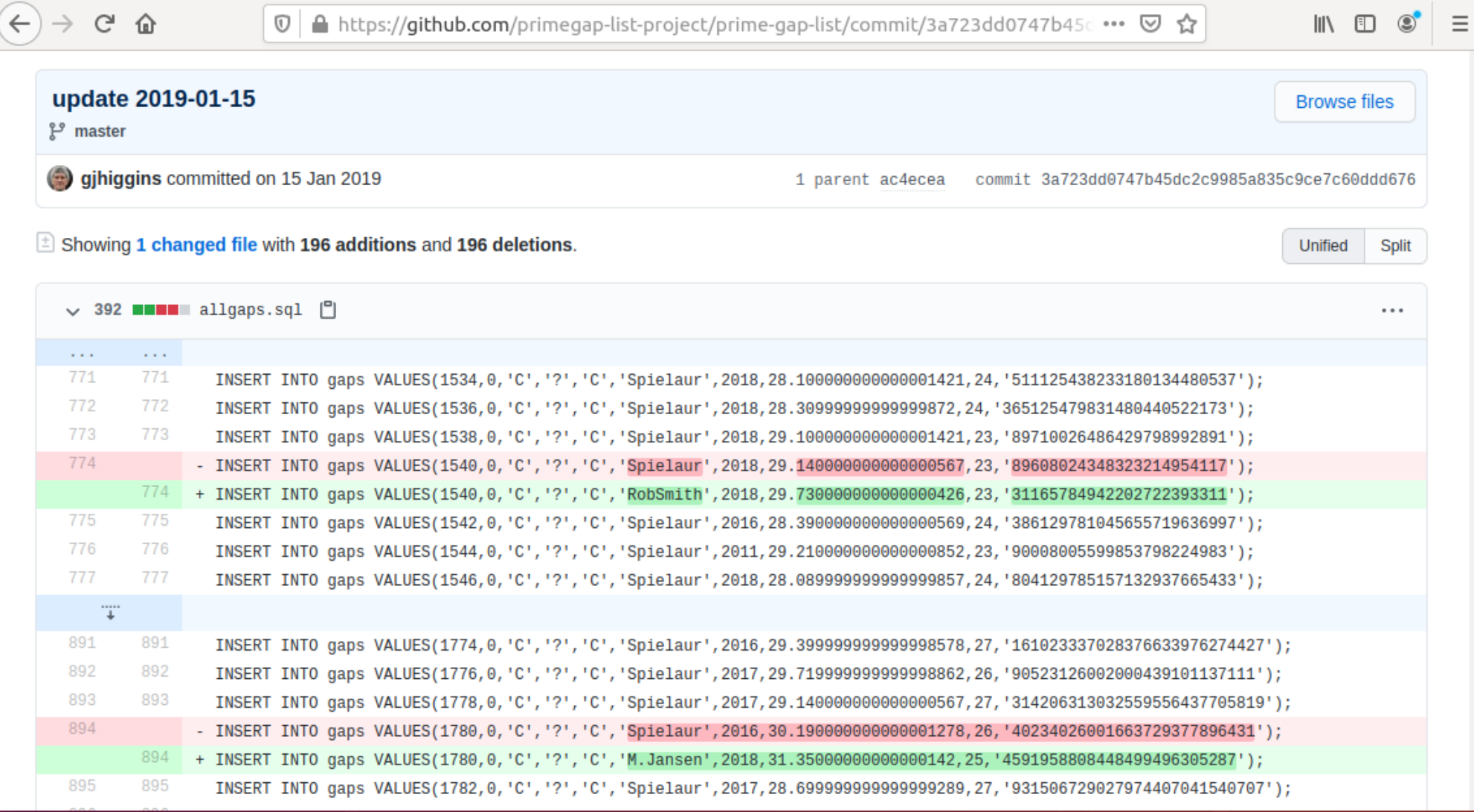
Screenshot of the prime gap list Github repository

The preservation of the earlier HTML pages is devolved to archive.org

An automated checking and submission service

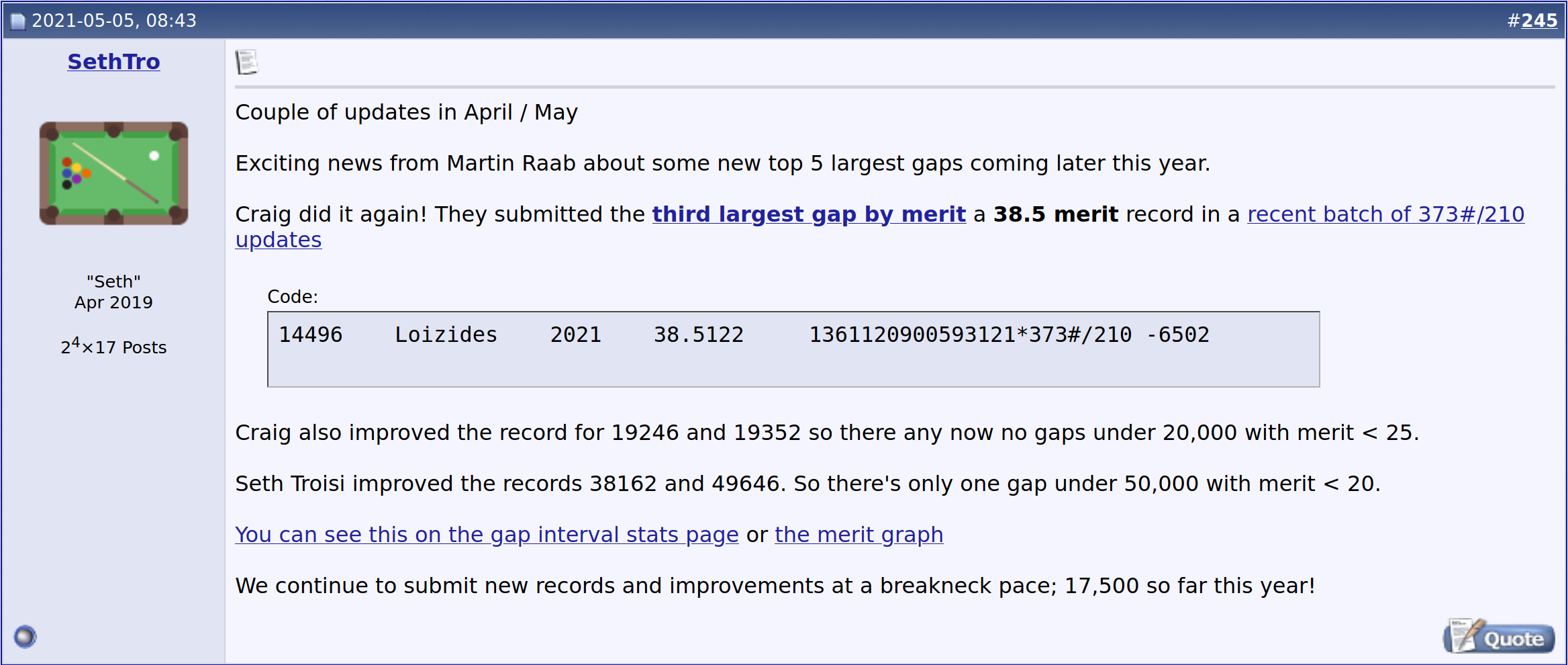
Subsquently, Seth Troisi of the PGS created an online service for the submission, automatic checking and recording of (those successful) candidate entries to the list of first known occurrence prime gaps

“I made a new website to verify records and automatically upload them to github. The first page performs some validity checks (merit > existing, prime < 10,000 digits) After you upload you'll see "1 Queued ... <data>" If you click the Watch Queue you can see it testing (if it's a larger record) and the results of previous tests. I only do PRP test for the endpoints. After the record is verified it’s immediately uploaded to the prime-gap-list github”Seth Troisi, in a post to the Mersenne Forum Prime Gap Search Group

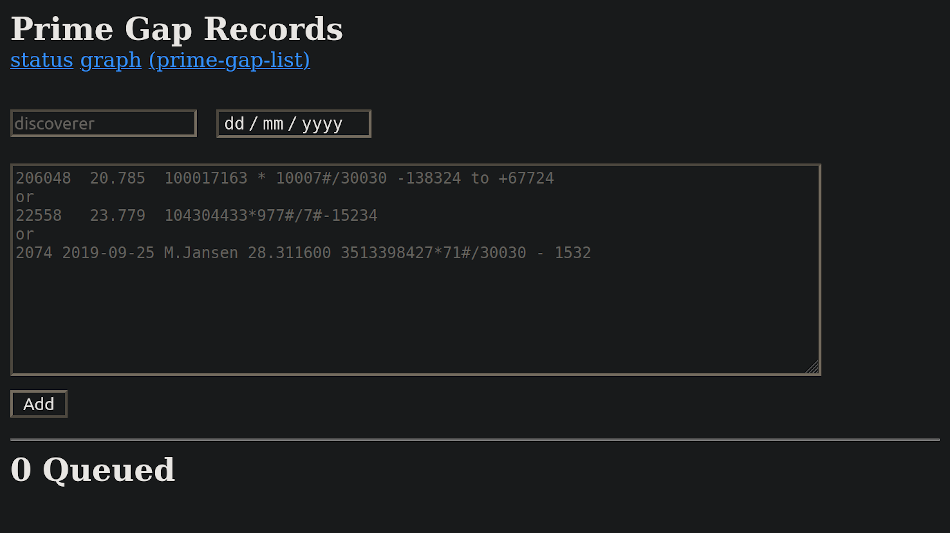
Screenshot of Seth Troisi’s online submission checking form

Still going strong

The current extent of the prime gap list is 101894 entries and the majority of the activity is concerned with improving merits but Martin Raab is still contributing extremely large gaps and has recently announced that he is working on a couple of 3M+ gaps.

prime gap list as SQL inserts

I’d like to believe that the current community curation of the table of first known occurrence prime gaps both reflects and meets the standards set and maintained for so many years by generations of contributors and particularly by Dr. Thomas Ray Nicely. Ave, Tom.

Previous Post Next Post